 |
| Huruf sigma besar |
Tip: Jika rumus tidak jelas pada tampilan mobile/hape, mintalah situs desktop/web pada browser Anda
Notasi sigma adalah penyingkatan penulisan penjumlahan menggunakan huruf Yunani, sigma besar (Σ).
Untuk memahami perlunya notasi sigma, perhatikan deret 10 bilangan asli pertama berikut ini.
Jika deret bilangan asli yang diperlukan sampai 20 suku, maka kita menuliskan
Wow…makin panjang. Sekarang jika deret yang diperlukan misalnya sampai 100 suku, 1000 suku, atau mungkin sampai sejuta suku tentu akan menghabiskan waktu , tenaga dan kertas kalau di buku atau memori kalau di perangkat elektronik. Oleh karena itulah untuk menyederhanakan penulisan maka dipakailah notasi sigma. Dengan notasi ini maka deret yang pertama dan yang kedua di atas bisa dituliskan sebagai
dan
Perhatikan , $i = 1$ menyatakan suku pertama pada penjumlahan diatas atau batas bawah, $i$ suku deret bilangan asli , dan 10 atau 20 diatas huruf sigma menyatakan suku terakhir atau batas atas penjumlahan tersebut.
Secara umum notasi sigma dapat didefinisikan sebagai berikut:
$\sum_{i=1}^{n}u_i$ dibaca: jumlah suku dari $i =1$ sampai $i = n$.
$i=1$: batas bawah penjumlahan
$n$: batas atas penjumlahan
$u_i$: suku deret yang berupa variable berindeks $i$
$i$: indeks
Contoh
Sifat-sifat linier notasi sigma
- $\sum_{i=1}^{n}k = kn$; $k$ tetapan
- $\sum_{i=1}^{n}ku_i = k\sum_{i=1}^{n}u_i$; $k$ tetapan
- $\sum_{i=1}^{n}u_i = \sum_{j=1}^{n}u_j$
- $\sum_{i=1}^{n}\left(u_i±v_i\right) = \sum_{i=1}^{n}u_i±\sum_{i=1}^{n}v_i$
- $\sum_{i=1}^{n}\left(u_i±v_i\right)^{2} = \sum_{i=1}^{n}u_i^2±\sum_{i=1}^{n}v_i^2$
- $\sum_{i=1}^{m}u_i+\sum_{i=m+1}^{n}u_i=\sum_{i=1}^{n}u_i$
- $\sum_{i=1}^{n}u_i=\sum_{i=2}^{n+1}u_{i-1}$
- $\sum_{i=n}^{n}u_i=u_n$
contoh
contoh
contoh
misal diketahui $u_i=2i$, jumlah lima suku pertamanya adalah
sekarang kita ganti $i$ dengan $j$, maka sukunya menjadi $u_j=2j$.Jumlah lima suku pertamanya adalah
jadi,
Contoh
a) penjumlahanb) pengurangan
Contoh
a) penjumlahanb) pengurangan
Contoh
Contoh
misal diketahui $u_i=4i$, jumlah lima suku pertamanya adalah
sekarang kita mindurkan $u_i$ satu langkah manjadi $u_i=4(i-1)$, jumlah dari suku kedua sampai suku ke enam adalah
jadi,
Contoh
misal diketahui $u_i=4i$, jumlah dua suku pertamanya adalahSekarang jika batas bawahnya dua, sama dengan batas atasnya, maka













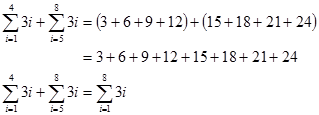








No comments:
Post a Comment